100-game
최근 코딩테스트 준비 겸 leetcode 문제를 풀다가 재밌는 문제를 발견했다. 이전에 수강했던 algorithmic game theory 라는 과목에서 배웠던 내용과 겹치는 것들 도 좀 있고, 적어두면 재밌을 것 같아 정리하기로 했다.
문제의 원본은 다음과 같다. https://leetcode.com/problems/can-i-win/
Can I win? 이란 문제에 나오는 100 game에 대해 간략히 설면하자면 두 명의 사람이 서로 번갈아가면서 1~10 의 숫자를 하나씩 말한다. 그리고 나온 숫자들을 더해갈 때, 누적 100 이상의 값을 처음으로 말하는 사람이 이기는 게임이다.
우리나라에서는 베스킨라빈스 31 로 유명한 게임과 같은 형식인 것 같다.
문제에서는 좀 더 복잡성을 위해서, 1~10 중 한 번 말한 값을 제외하게 (비복원 추출과 같게) 설정을 추가했다. 그리고 말할 수 있는 숫자의 범위와 최종 누적 값을 변경하는 두 개의 입력으로 주고 게임의 조건을 명시한다. 결국 주어진 두개의 자연수 입력에 대해서, player 1 이 그 게임을 이길 수 있냐는 질문에 답을 하는 게임이다.
중요한 조건 중 하나가 각자 player1, player2 는 optimal 하게 게임을 플레이 한다는 것이다. 이 조건이 게임 이론에서도 중요하게 작용하는데 이후에 추가 설명을 하려고 한다. 이길지 질지에 대한 결과를 미리 결정지을 수 있는 근거가 되는 기본 조건이다.
간단한 예시는 문제 원본 링크를 보면 알 수 있으니 (10, 100) 말고 다른 입력으로 조건이 주어졌을 때 player1 이 이길 수 있을지 한번 모든 경우를 따져보자.
1~4를 번갈아가며 중복없이 선택하고, 누적 합계 8이상을 먼저 말한 사람이 이기는 게임의 모든 경우를 나타낸 Tree 이다.
(4, 8) 의 게임에서는 처음 시작하는 Player 1이 1이나 2를 선택했다고 가정해보자. Player 2가 이어서 2나 1을 선택해서 누적합을 3으로 만든 후 차례를 넘기면 Player 1은 남은 선택지인 3이나 4로는 게임을 이길 수 없다.
반대로 Player 1이 처음에 3이나 4를 선택하면 어떤 경우에도 게임을 이길 수 있다.
그렇다면 이 게임에서는 Player 1 이 최적의 선택을 한다는 가정하에 항상 이길 수 있다는 결론이 나오는데, 이 값을 1이라고 하면 (질 경우는 -1이 될 것 이다.) 이 게임의 value 가 1이다 라고 얘기할 수 있다.
이와 같은 게임의 value를 알기위해서는 모든 경우를 조사해서 계산하면 얻을 수 있을텐데, 이를 Tree 형식으로 표현할 수가 있다. 각 노드에 넣은 값들은 다음을 의미하는데, 확대해서 확인해보길 바란다.
- 첫 줄의 숫자는 value. E는 게임이 끝났다는 표시로 임의로 정했다.
- 선택한 숫자들
- 현재 누적합
- 붉은 노드는 player 1의 차례, 푸른 노드는 player 2의 차례를 뜻한다.
- 각 edge에는 그 차례에 player가 어떤 숫자를 선택했는지 회색 수
설정을 조금 바꿔보자. (4, 9) 의 게임에서는 어떻게 될까? 방금 처럼 경우를 나눠서 하나씩 따져보자. 모든 경우에서 Player 2가 이기게 되므로 이 게임의 value 는 -1이다.
두번째 줄의 player2 경우들을 보면 모두 value가 -1인데, 처음 player1이 어떤 수를 부르더라도 모두 질 수밖에 없는 경우라는 뜻이된다.
만약 친구와 4-8 게임을 한다면 먼저 시작하고, 4-9 게임을 한다면 늦게 플레이 하는 사기를 칠 수도 있겠다.
게임이론
위의 예시에서 봤듯이, 이런 종류의 게임에는 항상 이기거나 지거나 (여긴 없지만 비기거나)의 결론이 날 것이고, 그 값 (게임의 value)를 특정지을 수 있다. 이런 게임의 종류라는 걸 좀 더 자세하게 다루면 다음과 같은 조건이 있다.
- two player 게임
- 서로 rational 해야하는데 이는 game theory 전체의 가정이기도 하다.
- perfect-information
- 서로 숨기는 정보가 없이 공유된다.
- sequential move
- 가위바위보 같이 동시에 move가 이뤄지는게 아니라 한 명씩 차례를 가지고 움직인다.
- 이런 게임은 위 처럼 Tree로 나타내면 보기 편한데 이를 Extensive form 이라고 한다.
- normal form 게임도 있는데 matrix로 표현하는 형태이고, 게임이론에서 매우 중요하게 다룬다.
- finite extensive form
- 게임이 끝나기는 해야한다. 체스나 바둑에서도 게임이 영원히 끝나는 것을 막는 룰이 있다.
- zero-sum 게임
- 이기거나 지거나 비기거나 밖에 없는 형태라고 보면 된다.
이런 조건을 만족하는 게임들이 여럿있는데, 위 문제의 게임도 이에 해당한다.
체스, 바둑, tic-tac-toe, 체커, connect4, 오델로 등도 해당된다.
이런 조건을 만족하는 게임들은 strongly determined 하다는 정리가 있는데 이 내용을 간단히 다루려 한다. 쉽게 말해 게임의 결론이 정해져 있다는 얘기다 (필승전략이 있다.?)
틱택토 같은 게임은 당연히 필승 전략이 있고 알기 쉬우나, 체스나 바둑은 그 결론이 뭔지 아직 알지 못한다. 아마 필승 전략없이 비기는 것이 최선의 선택(forcing a draw, game의 value가 0)이라고 추측하는 상태이다. 물론 game의 value를 알고 있다고 해서 그 게임이 재미가 없어지거나 의미가 없어지는 것을 아니라고 생각한다. 바둑같은 경우는 큰 범위의 경우의 수로도 유명한데, computing power의 한계가 있는 상태와 player의 심리전 등의 요소가 현실에서는 중요하게 작용한다고 생각한다.
determined의 개념에 추가로, value가 뭔지까지 밝혀진 경우 solved game 이라고 하는데, 여러 예시가 궁금하면 직접 찾아보길 바란다.
체커 일화로 재밌는 얘기가 있다.
Marion Tinseley 라는 수학 교수가 체커 게임 세계 챔피언이었다고 한다. 1992년도에 Chinook 라는 프로그램을 개발해서 이 교수와 경기를 붙였는데, 첫 매치는 4-2로 교수가 승리하고, 두번째 매치는 6번의 무승부 후 건강악화로 중단됐다고 한다. 교수가 이긴 경기중 60수 정도 앞서서 이길 수 있는 유일한 수를 둬서 이긴 경기도 있다고 하는데, 우리가 친숙한 알파고-이세돌 경기와 비슷한 사례가 이미 그보다 20년이나 앞서 있었다는 사실이 흥미로웠다. (IBM과 체스 챔피언 일화는 좀 더 유명할 지도 모르겠다.) 2007년이 되어서야 체커 게임이 컴퓨팅 파워로 모든 게임트리를 계산하면서 completely solved 되었다고 하는데, game의 value는 0이라고 한다. 양 플레이어가 최선의 선택을 한다면 결국 비기게 되는 게임이라고 볼 수 있다.
Chomp game
chomp 게임이라고 간단한 게임이 있는데, 이런 전략과 관련해서 생각해볼 만한 것이 있는데, strategy-stealing 이나 non-constructive proof 등의 내용이 흥미롭다. 규칙은 다음과 같다.
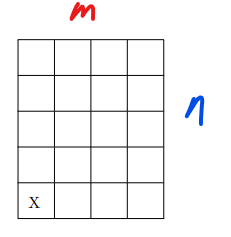
| chomp m by n | select gray cell |
|---|---|
 |
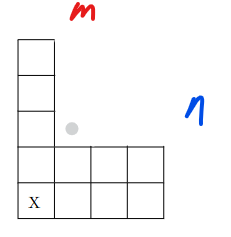 |
m by n 크기의 초콜릿? 이 있는데, 두명의 플레이어가 한 칸씩 선택한다. 선택한 칸과 같은 열과행을 포함한 우상향에 있는 모든 초콜릿은 선택한 사람이 먹는다. 좌하단 X 표시 칸의 초콜릿에는 독이 들어있는데, 그 칸을 먹은 사람이 지는 게임이다. 비기는게 없는 게임이다.
여기서도 초콜릿의 크기 m,n에 따라 다른 게임이 된다. 그럼 임의의 m,n에 대해서 필승 전략을 찾을 수 있을까? 한번 각자 생각해보고 게임을 해보길 바란다. 혹은 m=n일 때로 한정지어서 player 1의 필승전략을 찾아봐도 좋다.
m=n일때 필승전략 예시 보기
제시하는 방법은 수업때 들었던 한가지 전략이다. 먼저 X 바로 우상향 대각선 한칸을 선택해서 ㄴ자만 남기고 모든 초콜릿을 먹는다. player2가 ㄴ 자의 어느 칸을 먹던지 그와 대칭이 되도록 ㄴ의 반대편 부분을 선택해서 먹는다. 결국 독이든 칸은 player2가 먹게 된다.
일반적 m, n (1x1 제외)에서는 필승전략을 명시할 수 있을지 모르겠다. 하지만 player1이 이기는 필승전략은 존재한다! 바로 Non-constructive proof by contradiction 이라는 방식으로 증명을 하는건데, strategy-stealing이라는 전략이 토대가 된다.
먼저 P2가 이기는 필승 전략이 있다고 하자 (P1이 뭘하던지 진다는 뜻으로 game의 value가 -1 이라고 가정한 것이다.) 그럼 P1이 처음에 가장 우상단의 조각 하나를 선택해서 한칸의 초콜릿을 먹은 상황을 생각해보자. P2는 자신이 이길 수 있는 전략대로 선택을 할 것이다. (어딘지 모르겠지만 한 칸을 선택해서 먹을 것이다.)
그럼 다시 P1 의 차례인데, 그전에 여기서 오히려 과거로 돌아가서 P1이 처음에 우상단 한 칸을 선택하지 않고 P2가 선택한 필승의 그 칸을 미리 알고 선택해버릴 수 있다고 생각하는 것이다.(독심술을 쓰든 어떻게든 알아냈다고 치자) 그러면 이제 P1 이 필승 전략을 쓴 것과 동일한 상황이다. 근데 이는 모순이다. P1도 이기고 P2도 이기는 것이 불가능하기 때문.(사실 좀 더 엄밀히 증명하려면 Mini-max thm을 사용해야 한다.)
결국 game의 value가 -1이라고 한 가정이 잘못되었고 game의 value는 1이라는 증명이 끝난다(비기는게 없으므로)
Non-constructive와 strategy-stealing의 개념이 잘 이해되는 예시라고 생각한다. m=n일때 처럼 직접 전략을 찾아서 존재를 보인게 아니므로 non-constructive 하고, P2가 할 최선의 전략을 미치 훔친다는 측면에서 strategy-stealing 방식을 사용한 것이다. 여담으로 내쉬균형의 존재성 증명도 non-constructive한 방식으로 증명됐다.
strongly determined
좀 더 이론적인 내용을 다뤄보려 한다. 위에서부터 계속 game의 value에 대해서 말했는데, 이 값이 정확히 어떻게 나왔는지 알려면 몇가지 정리를 알아야 한다.
-
미니맥스 정리 : two-player, zero-sum 게임에서 성립하는 성질에 대한 내용이다. 일반적인 normal form game에서는 성립하지 않는 좋은 성질이 있다. 예를 들어 모든 상황에서 utility의 합이 0이기 때문에, 두개로 따로 표시할 필요가 없고 하나의 값만 사용하면 된다. (player2의 utility는 표시한 값의 음수를 취한 값으로 보고, bimatrix가 아니라 matrix로 표현된다는 뜻). v1과 v2라는 값을 먼저 정의해야 하는데, 쉽게 말하면 v1은 player2가 p1의 utility를 최소화 할때 p1이 그 와중에 자신의 utility를 최대화 할 수 있는 값이다. v2는 p2의 입장에서의 값에 음수를 취한 값이다. v1 = v2가 되면서 game의 value가 하나로 결정된다는 것이 정리의 내용인데, 이 value를 만드는 strategy는 pure일 필요는 없다.
- 현실에서 게임을 할때는 대부분 pure 전략만 생각하는데, 사실 게임의 균형을 생각할때는 여러 action에 확률을 주어 섞은 mixed strategy를 생각한다. 가위바위보 같은 게임에서는 각 확률 1/3씩 섞은 mixed strategy로 이루어진 strategy profile이 균형을 이루는 전략이 된다. 균형은 간단히 말하면 모든 player가 전략을 바꿀 유인이 없는 상태이다.
서로 rational한 agent 간의 zero-sum 게임에서는 결과가 determinant하다는 의미를 준다. 원래 p1은 v1과 v2 사이의 utility를 얻을 수 있고, 그 사이에서 선택을 하게된다고 볼 수 있는데, 그 두값이 같아져서 뭘 할지 명확해진다고 보면 된다.
이 미니맥스 정리부터 game theory가 시작되었다고 보면 된다고 배웠는데 그 만큼 여러 기반이 되는 정의나 개념들이 정립되었다고 한다.
미니맥스 정리는 1928 폰노이만이 발표한 정리인데 증명이 까다롭다고 한다.(찾아보진 않았다) 근데 1950 존 내쉬가 발표한 내쉬 균형의 존재성을 이용하면 쉽게 증명이 된다. -
셀튼 정리 : subgame perfect equilibrium에 대한 정리이다. subgame-perfect라는 개념은 extensive form game의 내쉬 균형이 그 게임의 모든 subtree에서도 균형인 것을 말한다.
모든 extensive form 게임은 pure subgame perfect equilibrium이 존재한다. 이 정리의 증명은 constructive 한 방식으로 증명이되는데, 실제로 pure subgame perfect equilibrium을 찾는 backward induction(끝부터 만들어가는 방식) 알고리즘을 제시해서 증명이 된다. -
체르멜로 정리 : 모든 extensive form, two-player, zero-sum game 이 strongly determinant하다는 정리이다. strongly determinant 개념은 pure strategies로 인해 얻어지는 unique value가 있다는 뜻이다. 이 정리는 위의 두 정리를 조합하면 얻어진다.
이 정리가 재밌는 점은 value가 뭔지는 모른다는 것이다. 위에도 말했듯이 체스 등의 게임은 value가 0이라고 추측하고 있다. 역사적으로는 white(first player)의 승률이 52%로 좀 더 우세하다고 한다.
다시 PS
처음 문제를 읽었을때는, 도대체 정답으로 원하는 값이 뭔지 알 수가 없었다.
player 1이 force a win이 가능하면 true를 아니면 false를 반환하라고 했는데, force a win이라는 개념이 잘 이해가 안갔다.
예를 들어 우리가 현실에서는 게임을 한다고 하면 누가이길지 모르고 50대50의 상황이라고 주로 생각을 한다. (축구를 한다거나, 스타크래프트 등의 게임을 한다거나). player 1이 항상 이길수 있는지의 여부가 결정적인지를 먼저 증명해야 이 문제에 답을 할 수 있을 것 같았고 그래서 그 상태를 inductive하게 구하는 방법을 생각한 다음에야 이해했다고 타협하고 넘어갈 수가 있었다. (이 문제의 핵심 로직이다. 한 칸 다음의 state들의 value를 알고 있다고 가정한 후, 현재 칸의 value를 결정하는 로직.)
그러다 문득 이전에 배운 game theory의 내용이 떠올라서 다시 그때의 노트를 찾아보니, 항상 1이거나 -1이라는 game의 value는 정해져 있다는 내용을 상기시킬 수 있었다. (이 게임에서는 비기는 결과가 없으니)
결론적으로 game theory의 사전지식이 없더라도 문제를 푸는데에 지장은 없지만, 알고보니 너무나도 전형적인 게임이론의 예시이고 이와 유사한 형태의 게임과 개념 특히 game tree나 sub game 등의 개념은 해법을 떠올리는데 도움이 분명히 된다.
실질적인 코딩으로 들어가보자. 문제에서 주어진 범위는 (20, 300) 까지로 매우 큰 편이라고 할 수 있다.
처음 봤던 것 처럼 모든 tree를 구한다고 하면 n! 의 경우를 모두 계산하게 되는데 이는 너무 큰 수치이다.
5만 보더라도 모든 Tree를 구하면 그림으로 나타내기도 어렵다.
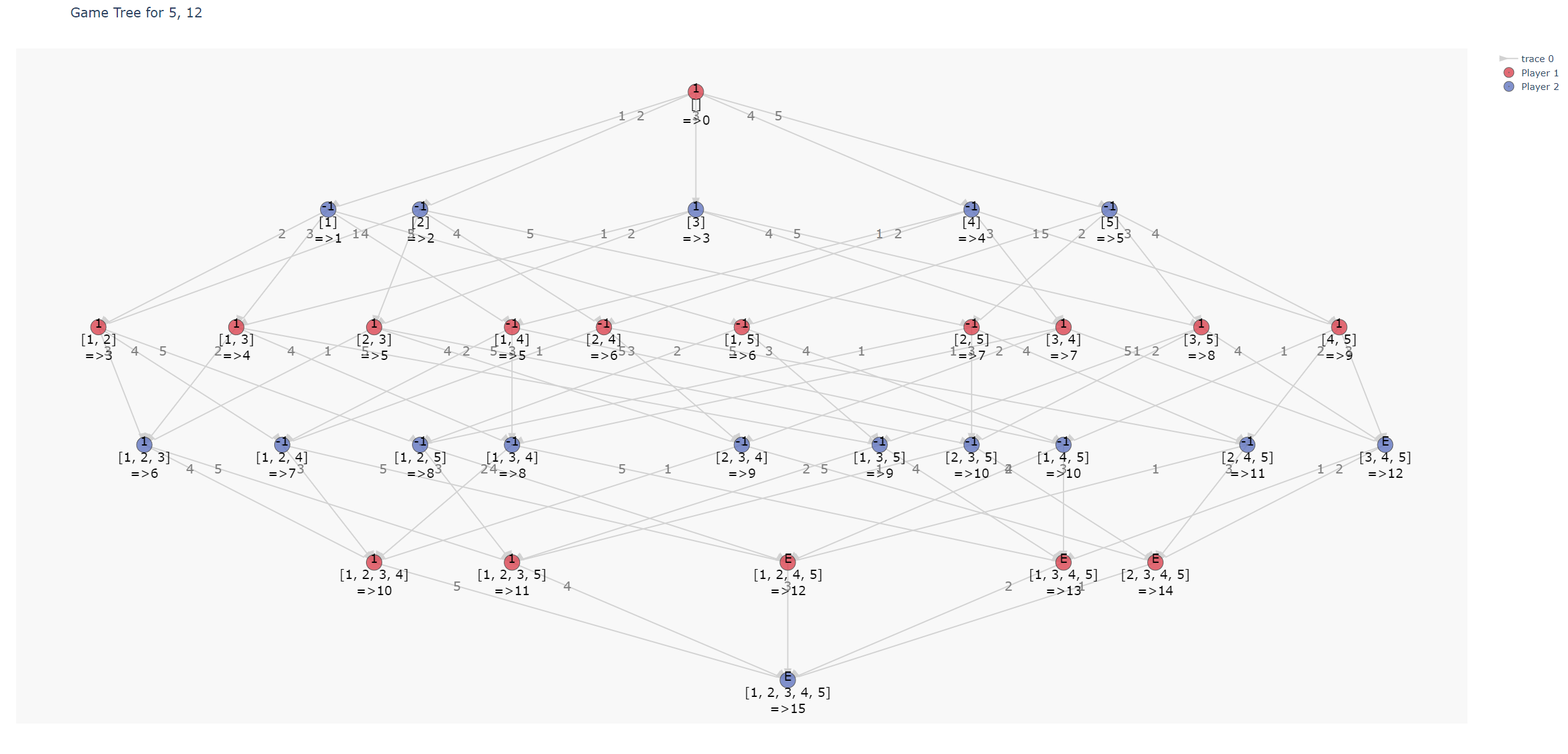
(5, 12)
이렇게 경우가 많은 문제를 해결할 때, 자주 쓰이는 technic이 있는데 그 중 두개가 이 문제에 적용 가능하다.
- dynamic programming
- back tracking
먼저 겹치는 경우들이 많은 경우 그 중복을 제거하는 방법이다. 예를들어 1->2->3을 선택한 상태나, 1->3>2를 선택한 상태는 동일하다. 이런 중복을 제거하면 계산을 상당히 줄일 수 있는데, 이미 계산된 state에 대해서는 계산하지 않도록 결과를 미리 저장해놓는 방법이 있다. memoization 이라고 하는 기법으로 state의 결과를 1 또는 -1로 저장하면 된다.
state는 1~n 중 각각의 수가 선택 되었는지 안되었는지를 나타내야 하므로 2^n개가 필요한데, 이는 bitwise한 연산과 표현을 사용하면 쉽게 state를 나타낼 수 있다.
(5, 12)
이처럼 중복을 제거하면 같은 정보를 더 compact하게 표현할 수 있다. (이제 tree가 아니라 state graph라고 보는게 맞다.)
두번째 방법으로는 back tracking인데, 이 그래프를 탐색할때 DFS 방식으로 탐색하는 것이다. 예를들어 player 1이 처음에 3을 선택하면 항상 이길 수 있다는 결과를 얻는데, 그 후 4나 5는 볼 필요도 없다는 뜻이다. 이런식으로 DFS 방식의 탐색을 하면, 원하는 결과가 나오지 않았으면 back tracking 방식으로 되돌아가고, 하나라도 찾으면 탐색을 종료해서 탐색하지 않아도 되는 경우를 제거할 수 있다. 문제 풀때는 backtracking으로 정답 하나만 찾으면 되지만 이 그래프를 그리려면 모든 탐색을 다 해야한다. 아래 시각화 코드에 예시 정답 몇개는 넣어놨다.
code
코드는 다음과 같다.
class Solution {
public:
int num_indices = 1048576;
vector<int> memo;
int max_choosable_int;
int desired_total;
bool canIWin(int maxChoosableInteger, int desiredTotal) {
max_choosable_int = maxChoosableInteger;
desired_total = desiredTotal;
int total_sum = (max_choosable_int*(max_choosable_int+1)/2);
if(total_sum < desired_total){
return false;
}
else if(total_sum == desired_total){
if(max_choosable_int % 2 == 1){
return true;
}else{
return false;
}
}
num_indices = 1<<max_choosable_int;
memo.resize(num_indices);
for(int i=0;i<num_indices;i++){
memo[i] = -1;
}
return P1CanForceWin(0, 0, 0);
}
int P1CanForceWin(int state, int state_sum, int bit_parity){
// std::cout << std::bitset<4>(state) << ": " << state_sum << std::endl;
if(memo[state] != -1){
return memo[state];
}
// int bit_count = 0;
// int state_sum = 0;
// for(int i=0;i<max_choosable_int;i++){
// if(state & (1<<i)){
// bit_count++;
// state_sum += (i+1);
// }
// }
// int bit_parity = bit_count % 2;
bool is_leaf = false;
if(state_sum + max_choosable_int >= desired_total){
for(int i=max_choosable_int-1;i>=0;i--){
if(!(state & (1<<i))){
if(state_sum + i+1 >= desired_total){
is_leaf = true;
break;
}
}
}
}
if(is_leaf){
memo[state] = !bit_parity;
return memo[state];
}
// even's turn -> bit_partiy = 0 ->
// if there exists s->s' s.t. f(s') == 1 exists, then f(s) = 1
if(bit_parity == 0){
bool exists_p1_win_in_next = false;
for(int i=0;i<max_choosable_int;i++){
if(!(state & (1<<i))){
if(P1CanForceWin(state | (1<<i), state_sum+i+1, !bit_parity) == 1){
exists_p1_win_in_next = true;
break;
}
}
}
memo[state] = static_cast<int>(exists_p1_win_in_next);
}else{
// odd's turn -> parity = 1 ->
// if f(s') == 1 for all s->s', then f(s) = 1
bool all_p1_win_in_next = true;
for(int i=0;i<max_choosable_int;i++){
if(!(state & (1<<i))){
if(P1CanForceWin(state | (1<<i), state_sum+i+1, !bit_parity) == 0){
all_p1_win_in_next = false;
break;
}
}
}
memo[state] = static_cast<int>(all_p1_win_in_next);
}
return memo[state];
}
};
그래프는 python으로 생성했다. (igraph, plotly 사용)
import igraph as ig
import matplotlib.pyplot as plt
import plotly.graph_objects as go
def GetVIdx(depth, left_order):
return acc_nPi[depth] + left_order
def GetFullGraph():
g = ig.Graph(num_vertices, directed=True)
max_choosable_int = n
state = 0
one_cnt = 0
same_depth_cnt = 0
q = []
q.append((state, one_cnt))
label = [0]*num_vertices
e_label = []
while(len(q) != 0):
state, one_cnt = q.pop(0)
depth = one_cnt
pidx = GetVIdx(depth, same_depth_cnt)
label[pidx] = state
num_children = n - depth
added_bits = []
for i in range(max_choosable_int):
nth_bit = 1<<i
if state & nth_bit == 0:
added_bits.append(i)
q.append((state | nth_bit, one_cnt+1))
edges_to_add = []
for child_cnt in range(num_children):
cidx = GetVIdx(depth+1, same_depth_cnt*num_children + child_cnt)
edges_to_add.append((cidx, pidx))
if(len(edges_to_add) > 0):
g.add_edges(edges_to_add)
e_label.extend(added_bits)
same_depth_cnt += 1
if(same_depth_cnt >= nPi[depth]):
same_depth_cnt = 0
g.vs["label"] = label
g.vs["size"] = 0.5
g.vs["label_size"] = 10
g.es["label"] = e_label
return g
def GetStateGraph():
g = ig.Graph(num_vertices, directed=True)
max_choosable_int = n
state = 0
one_cnt = 0
same_depth_cnt = 0
q = []
q.append((state, one_cnt))
label = [0]*num_vertices
e_label = []
visited = [0] * num_vertices
while(len(q) != 0):
state, one_cnt = q.pop(0)
if visited[state] != 0:
continue
visited[state] = 1
depth = one_cnt
pidx = state
label[pidx] = state
num_children = n - depth
added_bits = []
for i in range(max_choosable_int):
nth_bit = 1<<i
if state & nth_bit == 0:
added_bits.append(i)
q.append((state | nth_bit, one_cnt+1))
edges_to_add = []
for child_cnt in range(num_children):
cidx = state | (1<<added_bits[child_cnt])
edges_to_add.append((cidx, pidx))
if(len(edges_to_add) > 0):
g.add_edges(edges_to_add)
e_label.extend(added_bits)
same_depth_cnt += 1
if(same_depth_cnt >= nPi[depth]):
same_depth_cnt = 0
g.vs["label"] = label
g.vs["size"] = 0.5
g.vs["label_size"] = 10
g.es["label"] = e_label
return g
def make_annotations(pos, text, font_size=10, font_color='rgb(250,250,250)', offset=0):
L=len(pos)
if len(text)!=L:
raise ValueError('The lists pos and text must have the same len')
annotations = []
for k in range(L):
annotations.append(
dict(
text=text[k], # or replace labels with a different list for the text within the circle
x=pos[k][0], y=pos[k][1]-offset,
xref='x1', yref='y1',
font=dict(color=font_color, size=font_size),
showarrow=False)
)
return annotations
def count_ones(bit):
cnt = 0
for i in range(n):
if bit & (1 << i):
cnt += 1
return cnt
def convert_state_to_string(state):
selected = []
for i in range(n):
if state & (1 << i):
selected.append(i+1)
value = can_win[state]
if value == 0:
value = -1
elif value == 2:
value = 'E'
msg = f"{value}<br>["
msg += ", ".join(list(map(str, selected)))
msg += f"]<br>=>{sum(selected)}"
return msg
if __name__ == "__main__":
# 5-11
# can_win = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 2, 1, 0, 2, 2, 2, 2, 2, 2, ]
# 5-12
can_win = [1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 2, 2, 2, 2, ]
# 4-8
# can_win = [1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 2, 2, 2, ]
# 4-9
# can_win = [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 2, 2, ]
# 10-12
# can_win = [1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 2, 2, 2, 2, 2, 0, 1, 1, 0, 1, 0, 0, 2, 1, 0, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 1, 1, 0, 1, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 1, 1, 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, ]
# 10-20
# can_win = [1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 2, 2, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 2, 2, 2, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 2, 2, 2, 2, 2, 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 2, 2, 2, 2, 2, 1, 0, 0, 1, 0, 1, 1, 2, 0, 1, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 1, 0, 1, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 2, 0, 1, 2, 2, 2, 2, 2, 2, 1, 0, 0, 1, 0, 1, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 1, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 2, 1, 0, 0, 1, 0, 1, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 1, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, ]
print(len(can_win))
n = 5
desired_total = 12
nPi = [1]
for i in range(n):
nPi.append(nPi[-1]*(n-i))
acc_nPi = [0]
for i in range(n+1):
acc_nPi.append(acc_nPi[-1] + nPi[i])
# full graph
# num_vertices = acc_nPi[n+1]
# g = GetFullGraph()
# state graph
num_vertices = 1 << n
g = GetStateGraph()
# fig, ax = plt.subplots()
# # ig.plot(g, layout="kk", target=ax)
# ig.plot(g, layout=g.layout_reingold_tilford(mode="in", root=[0]), target=ax)
# plt.show()
v_label = list(map(str, range(num_vertices)))
# lay = g.layout_reingold_tilford(mode="in", root=[0])
lay = g.layout_sugiyama()
position = {k: lay[k] for k in range(num_vertices)}
Y = [lay[k][1] for k in range(num_vertices)]
M = max(Y)
es = ig.EdgeSeq(g) # sequence of edges
E = [e.tuple for e in g.es] # list of edges
# pos_y_map = lambda y: 2*M-y
pos_y_map = lambda y: y
L = len(position)
Xn = [position[k][0] for k in range(L)]
Yn = [pos_y_map(position[k][1]) for k in range(L)]
v_annotation_pos = list([x,y] for x,y in zip(Xn, Yn))
Xe = []
Ye = []
edge_label_pos = []
for edge in E:
x1 = position[edge[0]][0]
y1 = pos_y_map(position[edge[0]][1])
x2 = position[edge[1]][0]
y2 = pos_y_map(position[edge[1]][1])
Xe+=[x2, x1, None]
Ye+=[y2, y1, None]
edge_label_pos.append([(x1*0.1+x2*0.9), (y1*0.1+y2*0.9)])
edge_label = [str(l+1) for l in g.es["label"]]
fig = go.Figure()
fig.add_trace(go.Scatter(x=Xe,
y=Ye,
mode='lines+markers',
line=dict(color='rgb(210,210,210)', width=2),
hoverinfo='none',
marker=dict(size=20,
symbol= "arrow",
angleref="previous"),
)
)
Xn1 = []
Yn1 = []
label1 = []
Xn2 = []
Yn2 = []
label2 = []
print(g.vs["label"])
for i in range(num_vertices):
state = g.vs["label"][i]
bit_count = count_ones(state)
if bit_count % 2 == 0:
Xn1.append(Xn[i])
Yn1.append(Yn[i])
label1.append(i)
else:
Xn2.append(Xn[i])
Yn2.append(Yn[i])
label2.append(i)
fig.add_trace(go.Scatter(x=Xn1,
y=Yn1,
mode='markers',
name='Player 1',
marker=dict(symbol='circle-dot',
size=25,
color='#DB4551',
line=dict(color='rgb(50,50,50)', width=1)
),
text=label1,
hoverinfo='text',
opacity=0.8
))
fig.add_trace(go.Scatter(x=Xn2,
y=Yn2,
mode='markers',
name='Player 2',
marker=dict(symbol='circle-dot',
size=25,
color='#6175c1', #'#DB4551',
line=dict(color='rgb(50,50,50)', width=1)
),
text=label2,
hoverinfo='text',
opacity=0.8
))
axis = dict(showline=False, # hide axis line, grid, ticklabels and title
zeroline=False,
showgrid=False,
showticklabels=False,
)
v_label = list(map(convert_state_to_string, g.vs["label"]))
annotations = make_annotations(
v_annotation_pos, v_label, 10, "black", 0
) + make_annotations(
edge_label_pos, edge_label, 10, "gray"
)
fig.update_layout(title=f'Game Tree for {n}, {desired_total}',
annotations=annotations,
font_size=15,
showlegend=True,
xaxis=axis,
yaxis=axis,
margin=dict(l=40, r=40, b=85, t=100),
hovermode='closest',
plot_bgcolor='rgb(248,248,248)'
)
# fig.show()
fig.write_html("game-tree.html")